利率上限是指买卖双方就未来某一时期商定一个固定利率作为利率上限，如果协议规范的市场利率(通常为LIBOR)超过上限利率，则由卖方将市场利率与上限利率的差额支付给买方，但买方在协议签订时，必须支付卖方一定费用。

具备浮动利率负债的债务人，或具备固定利率存款的债权人，为防止利率危机，固定债务(权)的支出(或收入)，常使用这一工具，以规避危机，核算成本。

假设上限利率为Rx，贷款本金额为L，利息在时间T、2T、3T、…、nT时支付，T为以年为单位表示的时间长度，通常为3个月(0.25年)或半年。在时间(k+1)T时，利率上限的卖方所要作出的支付为：

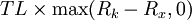
其中Rk为时间kT时的LIBOR利率。假设Fk为时间kT至(k+1)T之间的远期利率，我们可以视之为折现率将上面的现金流折现到时间kT，折现值则为：

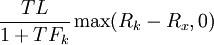
如果我们注意到，在时间kT时，Fk = Rk，则上式又可改定为：

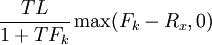
这样，我们就可将一个利率上限看作由若干期限期权组成，每个期权的标的物为一关于Fk的远期利率合约，期限从时间。到kT，本金金额为TL / (1 + TFk)，执行价格为Rx。

如果我们假设在期权期限内，Fk的标准方差σF恒定不变，那么根据期货期权的B-S定价模型，每个期权的价格为：

(1) 其中：

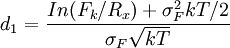
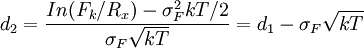
r为时间0至时间kT之间的以连续利率形式表达的无风险利率，如果我们定义r为时间0至时间(k+1)T之间的无风险利率，则式(1)可等效改写为：

TLe − r(k + 1)T[FkN(d1) − RxN(d2)]

在计算出所有期权价格后，将其相加，我们便得到一个利率上限的价格。

B-S定价模型的一个假设便是σF恒定，这充其量是对实际情况一种近似。如果一个远期合约距到期日时间较长，F对当前利率变化并不敏感，其标准差σF也较低。但是随着远期合约逐渐趋近到期日，F就变得对当前利率变化越来越敏感，σF也随之不断增加。

在实践中，人们采用以下步骤来弥补B-S模型的不足：首先，将B-S模型应用于欧洲美元期货期权，反解出期货期权报价所暗含的σF。欧洲美元期货期权的期限应与所要计算的期权的期限一样，其次，将此σF代入B-S模型再去求解利率上限中期权的价格。这种以实际市场交易价格中反求σF的方法，可以降低模型所带来的误差。

当利率上限所含的某种期权的期限超过所有欧洲美元期货期权寸，我们就只能用插值法来估计其σF了。有些时候，实务操作人员设定一个适用于所有期权的σF，然后根据各期权的期限长度对其进行调整。调整后的σF才被用于实际计算。

在一笔利率上限交易中，交易双方通常需要明确以下主要内容。

交易货币和金额：通常是借款人的借款本金。

有效期限：借款人需要防范利率危机的期限。

执行价格：借款人可以承担的最高利率水平。

付息期限：借款人付息的期限，即每个设定日期间的时间间隔，通常采用伦敦同业放款利率的期限，如3个月付息一次，6个月付息一次等等。

参考利率：作为市场利率水平，通常采用各期的伦敦同业放款利率。

利率上限的期权费通常采取一次性方式支付，其报价与利率期权的期权费报价方式有所区别。如借款人买入一项利率上限，金额1000万美元，有效期限为3年，执行价格6％，参考利率为3个月伦敦同业放款利率，期权费报价为1．5％。则实际需支付的期权费金额为：

10000000×1．5％=150000(美元)

其中，S：每期交割金额；

A：利率上限交易金额；

L：参考利率水平；

K：执行价格；

T：每个付息期限的天数；

B：1年的天数，取360或365，根据区别的货币和区别的市场惯例而定。

当L大于K时，卖方向买方支付S金额，当L小于或等于K时，交易双方不发生资金收付。利率上限每一期的交割金额通常在期末才发生。但在某些状况下，交易双方可约定在期初支付，此时交割金额必须按参考利率计算出期初的贴现金额，其原理同远期利率协议相同。